Bridge Analysis

This notebook demonstrates the use of PyCBA in conducting moving load and other analyses relevant to bridge analysis.

import pycba as cba
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from IPython import display

Example 1 - Moving Load Envelope

This example shows the basic interface for moving a vehicle across the bridge.

Consider a two-span continuous bridge, 50 m long:

L = [25, 25]
EI = 30 * 1e11 * np.ones(len(L)) * 1e-6
R = [-1, 0, -1, 0, -1, 0]

and a three-axle vehicle with a 6 t steer axle, 6 m spacing back to the tandem of 12 t axles each with spacing 1.2 m:

axle_spacings = np.array([6, 1.2])
axle_weights = np.array([6, 12, 12]) * 9.81  # t to kN

Now define the bridge_analysis object and add the bridge definition and vehicle definitions:

bridge_analysis = cba.BridgeAnalysis()
bridge = bridge_analysis.add_bridge(L, EI, R)
vehicle = bridge_analysis.add_vehicle(axle_spacings, axle_weights)

Examine the vehicle at a single position, when the front axle is at 30.0 m say:

bridge_analysis.static_vehicle(30.0, True);

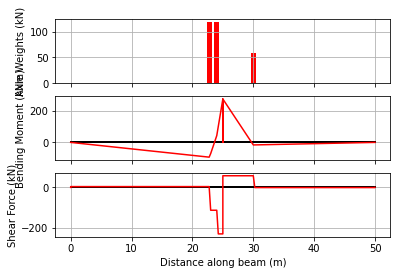
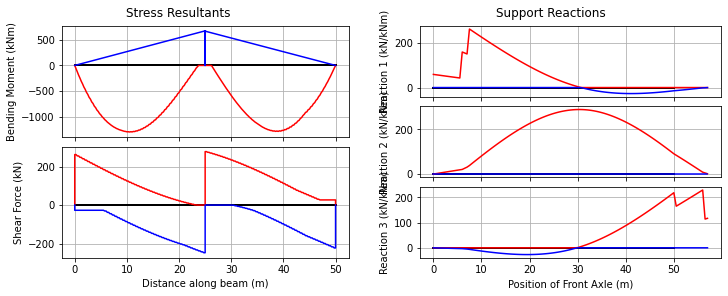
Now we run the vehicle over the bridge, returning the envelope of results. When run as a python script, the matplotlib figure will animate each result when plot_all=True.

bridge_analysis.run_vehicle(0.5, plot_env=True, plot_all=False);

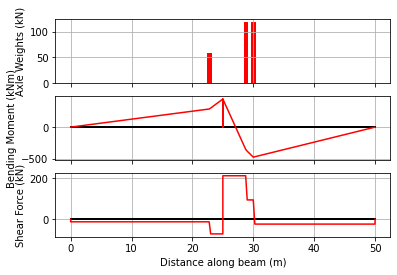
Alternatively, using the reverse() method, we can do an analysis for the vehicle travelling in the reverse direction.

vehicle.reverse()
bridge_analysis.static_vehicle(30.0, True)

<pycba.results.BeamResults at 0x7fdac318a430>

Example 2 - Critical Values and Positions

L = [37]
EI = 30 * 1e11 * np.ones(len(L)) * 1e-6
R = [-1, 0, -1, 0]

bridge = cba.BeamAnalysis(L, EI, R)
bridge.npts = 500  # Use more points along the beam members
vehicle = cba.VehicleLibrary.get_m1600(6.25)
bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
env = bridge_analysis.run_vehicle(0.1)

From the envelope, we can extract the critical values of load effects, where they are located, and the vehicle position that caused it:

cvals = bridge_analysis.critical_values(env)

and so if we are interested in the maximum bending moment in particular, we can interogate the results as follows:

pos = cvals["Mmax"]["pos"][0]
at = cvals["Mmax"]["at"]
val = cvals["Mmax"]["val"]
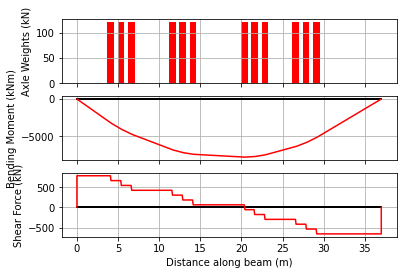
print(f"Max moment is {val} kNm at {at:.2f} m when front axle position is {pos} m")

Max moment is 7809.3 kNm at 20.35 m when front axle position is 29.1 m

and confirm the results with a static analysis with the vehicle at that position:

bridge_analysis.static_vehicle(pos, True);

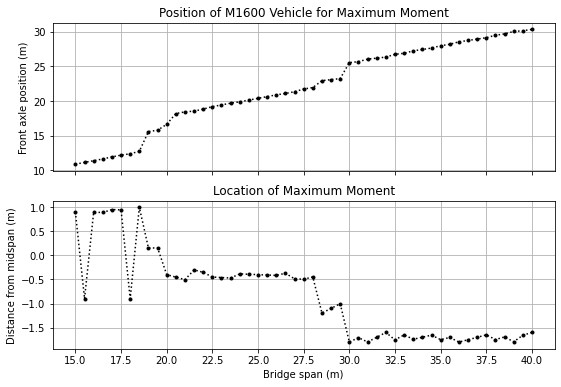
Example 3 - Critical M1600 Positions

Here we consider the positioning of the M1600 vehicle to obtain maximum bending moment in simply-supported bridges of spans 15 to 40~m

First create the array to store the results and the span lengths.

critical_axle_positions = []
critical_beam_location = []
spans = np.arange(15,40.5,0.5)

Next, create unchanging variables outside the loop, and then loop to find the critical positions:

vehicle = cba.VehicleLibrary.get_m1600(6.25)
for L in spans:
    EI = 30 * 1e11 * 1e-6
    R = [-1, 0, -1, 0]
    bridge = cba.BeamAnalysis([L], EI, R)
    bridge.npts = 500  # Use more points along the beam members
    bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
    env = bridge_analysis.run_vehicle(0.05)
    cvals = bridge_analysis.critical_values(env)
    critical_axle_positions.append(cvals["Mmax"]["pos"][0])
    critical_beam_location.append(cvals["Mmax"]["at"])

And plot the results

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(9,6), sharex=True)
ax1.plot(spans,critical_axle_positions,'k.:')
ax1.grid(which="both")
ax1.set_ylabel("Front axle position (m)")
ax1.set_title("Position of M1600 Vehicle for Maximum Moment");

ax2.plot(spans,spans/2 - critical_beam_location,'k.:')
ax2.grid(which="both")
ax2.set_title("Location of Maximum Moment")
ax2.set_ylabel("Distance from midspan (m)")
ax2.locator_params(axis='x', nbins=12)
ax2.set_xlabel("Bridge span (m)");

Example 4 - Access Assessment for Single Vehicles

This example considers the relative load effects between a reference vehicle and another vehicle. This type of analysis is commonly done to assess whether a new vehicle type would impose more onerous load effects on a bridge than some existing reference vehicle.

L = [25, 25]
EI = 30 * 1e11 * np.ones(len(L)) * 1e-6
R = [-1, 0, -1, 0, -1, 0]
bridge = cba.BeamAnalysis(L, EI, R)

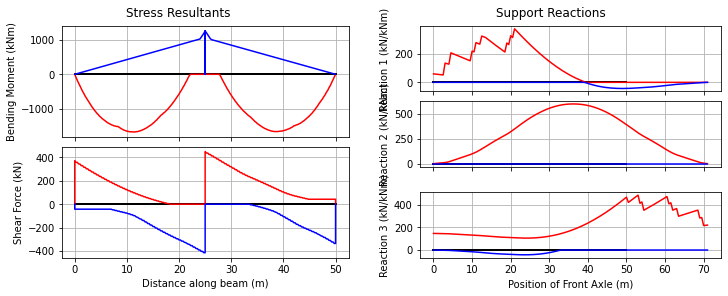
Here we use a suite of reference vehicles (the Australian ABAG B-doubles) to create a “super-envelope”: an envelope of the load effect envelopes from each of the 3 reference vehicles.

Firstly, obtain the vehicle from the VehicleLibrary and analyze for the envelope, appending it to the list of envelopes.

envs = []
for i in range(3):
    vehicle = cba.VehicleLibrary.get_abag_bdouble(i)
    bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
    envs.append(bridge_analysis.run_vehicle(0.5))

Next, create a new zero-like envelope and augment it with the stored envelopes, such that the result is the envelope of envelopes:

envenv = cba.Envelopes.zero_like(envs[0])
for e in envs:
    envenv.augment(e)
bridge_analysis.plot_envelopes(envenv)

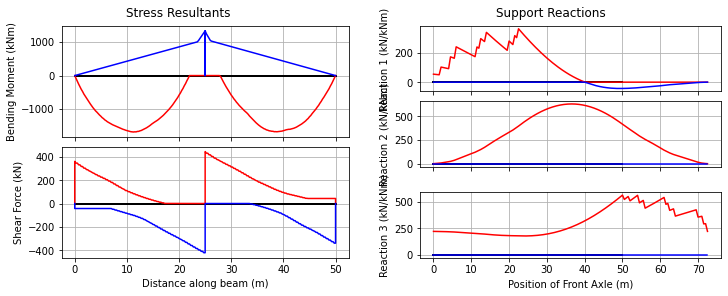
Now analyze the permit application vehicle; here just taking an example vehicle from the VehicleLibrary:

vehicle = cba.VehicleLibrary.get_example_permit()
bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
trial_env = bridge_analysis.run_vehicle(0.5, True)

And we can plot the ratios of trial to reference envelopes

envr = bridge_analysis.envelopes_ratios(trial_env, envenv)
bridge_analysis.plot_ratios(envr)

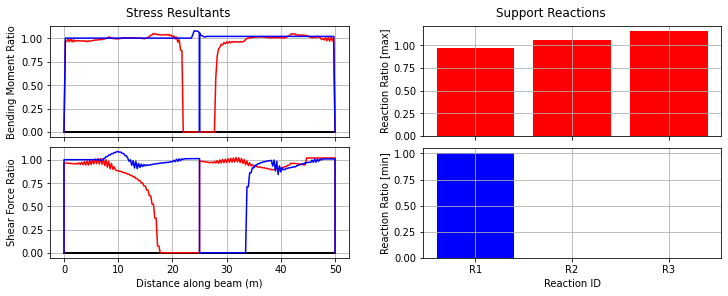
As can be seen in this case, the central support reaction is greater than 1.0, as is the hogging moment (by about 7%). This vehicle is unlikely to be granted a permit as a result.

Example 5 - Access Assessment for Vehicle Spacings

Using the make_train method we create a Vehicle object representing a sequence of vehicles at different spacings. Here, we will explore different prime mover and platform trailer combinations commonly adopted in “superload” transport convoys.

First set up the bridge as per Example 3:

L = [25, 25]
EI = 30 * 1e11 * np.ones(len(L)) * 1e-6
R = [-1, 0, -1, 0, -1, 0]
bridge = cba.BeamAnalysis(L, EI, R)

And now define the components of the superload:

prime_mover = cba.Vehicle(axle_spacings=np.array([3.2,1.2]),
                          axle_weights=np.array([6.5,9.25,9.25])*9.81)
platform_trailer = cba.Vehicle(axle_spacings=np.array([1.8,]*9),
                               axle_weights=np.array([12]*10)*9.81)

Three spacing combinations are explored for a convoy comprising of two front prime movers followed by two platform trailers and then two back prime movers.

inter_spaces = [np.array([5.0,6.3,8.0,6.0,4.8]),
               np.array([4.8,6.0,7.5,6.0,5.0]),
               np.array([5.0,6.3,8.0,6.3,5.0])]

Now, similar to Example 3, run the analysis for each set of spacings and store the envelopes:

envs = []
for s in inter_spaces:
    vehicle = cba.make_train([prime_mover]*2 + [platform_trailer]*2 + [prime_mover]*2,spacings=s)
    bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
    envs.append(bridge_analysis.run_vehicle(0.1))

And now augment the envelopes to get the overall envelope:

envenv = cba.Envelopes.zero_like(envs[0])
for e in envs:
    envenv.augment(e)
bridge_analysis.plot_envelopes(envenv)

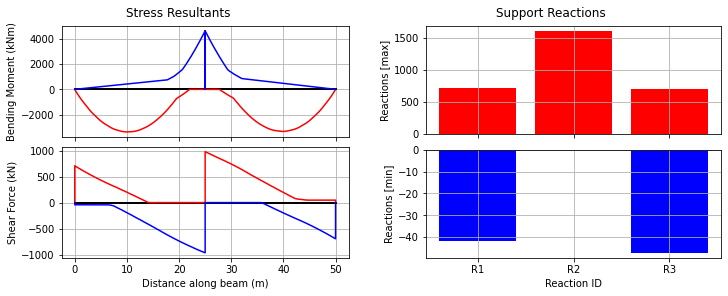
Note that this overall envelope can only show the extremes of reaction values, since the time histories of reactions are not compatible.

Example 6 - Rail loading

Using the VehicleLibrary.get_la_rail method we create a 300LA train load and calculate the values for Appendix C of AS5100.2.

First, create the vehicle using the library method, here the defaults of 300LA, 12m axle-group spacing (centre-to-centre), and 10 No. axle groups (length 150~m) are adequate. Note that we could rationalize the number of axle groups for shorter spans to reduce computation, but this is just a refinement.

vehicle = cba.VehicleLibrary.get_la_rail()

Next create the list of spans we wish to analyse (all simply-supported), and we’ll store the results for each span in a list for bending moment, shear, and reactions.

Here we’ll just do from 10 to 100~m spans in 10~m increments, but all 99 spans could be done.

spans = np.arange(10,101,10)
M = []
V = []
R = []

Now loop over each span and calculate the load effects

for s in spans:
    L = [s]
    # Simply-supported with arbitrary EI
    bridge = cba.BeamAnalysis(L, 30e6, [-1, 0, -1, 0])
    bridge.npts = 500  # Use more points along the beam
    bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
    env = bridge_analysis.run_vehicle(0.1)
    cvals = bridge_analysis.critical_values(env)
    m = cvals["Mmax"]["val"]
    v = max(cvals["Vmax"]["val"], abs(cvals["Vmin"]["val"]))
    r = max(cvals["Rmax0"]["val"], cvals["Rmax1"]["val"])
    # now round to nearest 5 as code does
    M.append(round(m / 5) * 5)
    V.append(round(v / 5) * 5)
    R.append(round(r / 5) * 5)

The reason for calculating the shear and reaction is that the vehicle step distance can cause differences. The 0.1~m value selected here is quite small, especially for longer bridges, and so could be different to that used for generating the values in the code. Between the shear and reaction results, the code values should be replicated.

To display the results in a nice way, we use pandas and create a dataframe.

results = list(zip(spans, M, V, R))
columns = ["Span (m)", "Moment (kNm)", "Shear (kN)", "Reaction (kN)"]
df = pd.DataFrame(results,columns=columns,index=spans)

Let’s have a look at the results, without showing the redundant index:

df.style.hide()

Span (m)	Moment (kNm)	Shear (kN)	Reaction (kN)
10	2400	1040	1050
20	6300	1515	1530
30	12515	2005	2015
40	21555	2505	2515
50	32560	3015	3025
60	46405	3525	3535
70	62385	4025	4035
80	81045	4525	4535
90	102740	5020	5030
100	126300	5515	5525

Example 7 - AS5100.2 Appendix C

First we will write a function that accepts a vehicle, loops over a specified span range extracting the critical load effects, and returns a pandas dataframe of the results. We can then use this function for both road and rail.

The function accepts the low and high spans of the range to consider. While the code examines from 1 to 100 m spans, this takes a while to compute, so for the present purposes, facilitate considering a smaller range.

The function also accepts a UDL, necessary for the road bridges. This UDL is applied to the BeamAnalysis object and retained in the BridgeAnalysis object and applied throughout the vehicle traverse.

We will record both shear and reactions, which can vary slightly due to the step spacing of the load as it traverses the beam.

def critical_effects(vehicle,low_span=1,high_span=100,udl=0):
    spans = np.arange(low_span,high_span+1,1)
    M = []
    V = []
    R = []
    for L in spans:
        # Simply-supported with arbitrary EI
        bridge = cba.BeamAnalysis([L], 30e6, [-1, 0, -1, 0])
        bridge.npts = 500  # Use more points along the beam
        bridge.add_udl(i_span=1,w=udl)  # Add any UDL
        bridge_analysis = cba.BridgeAnalysis(bridge, vehicle)
        env = bridge_analysis.run_vehicle(0.1)  # small step

        # Extract critical values
        cvals = bridge_analysis.critical_values(env)
        m = cvals["Mmax"]["val"]
        v = max(cvals["Vmax"]["val"], abs(cvals["Vmin"]["val"]))
        r = max(cvals["Rmax0"]["val"], cvals["Rmax1"]["val"])

        # now round to nearest 5 as code does
        M.append(round(m / 5) * 5)
        V.append(round(v / 5) * 5)
        R.append(round(r / 5) * 5)

    results = list(zip(spans, M, V, R))
    columns = ["Bridge_length", "m", "v", "r"]
    df = pd.DataFrame(results,columns=columns,index=spans)
    return df

Let’s examine the range 40 to 50 m here:

low_span = 40
high_span = 50

First, we examine the road loading in Table C1 of the code, considering the moving and stationary load models seperately:

m1600_vehicle = cba.VehicleLibrary.get_m1600(6.25)
df_m1600 = critical_effects(m1600_vehicle,low_span=low_span,high_span=high_span,udl=6)
df_m1600

	Bridge_length	m	v	r
40	40	10070	1120	1120
41	41	10490	1130	1135
42	42	10910	1145	1150
43	43	11330	1160	1160
44	44	11755	1170	1175
45	45	12180	1180	1185
46	46	12605	1195	1195
47	47	13030	1205	1210
48	48	13465	1215	1220
49	49	13895	1225	1230
50	50	14325	1235	1240

s1600_vehicle = cba.VehicleLibrary.get_s1600(6.25)
df_s1600 = critical_effects(s1600_vehicle,low_span=low_span,high_span=high_span,udl=24)
df_s1600

	Bridge_length	m	v	r
40	40	10695	1145	1150
41	41	11180	1165	1165
42	42	11665	1185	1185
43	43	12160	1200	1205
44	44	12660	1220	1220
45	45	13165	1240	1240
46	46	13675	1255	1260
47	47	14195	1275	1275
48	48	14720	1290	1290
49	49	15245	1305	1310
50	50	15785	1325	1325

Next, let’s examine the 300LA results shown in Table C2 of the code.

rail_vehicle = cba.VehicleLibrary.get_la_rail(axle_weight=300)
df_rail = critical_effects(rail_vehicle,low_span=low_span,high_span=high_span)
df_rail

	Bridge_length	m	v	r
40	40	21555	2505	2515
41	41	22545	2555	2565
42	42	23535	2610	2620
43	43	24520	2665	2675
44	44	25510	2720	2735
45	45	26525	2775	2785
46	46	27590	2825	2840
47	47	28790	2875	2890
48	48	30000	2925	2935
49	49	31270	2970	2980
50	50	32560	3015	3025

From the results, it can be seen that the values in the code differ somewhat. Presumably this is because the values in the code were calculated using a coarser increment in the vehicle position for the traverse.